1. What is a Drift Velocity Calculator?

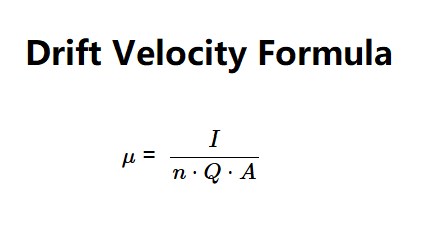
Definition: This calculator computes the drift velocity (\( \mu \)) of electrons in a conductor based on the current (\( I \)), charge of an electron (\( Q \)), number of electrons per unit volume (\( n \)), and cross-sectional area of the wire (\( A \)).

Purpose: It is used in physics and electrical engineering to determine the average velocity of electrons moving through a conductor under the influence of an electric field, which is essential for understanding current flow and conductor behavior.

2. How Does the Calculator Work?

Drift velocity is calculated using:

Current conversions:

• A: Direct use
• mA: A = mA × 0.001

Charge conversions:

• C: Direct use
• µC: C = µC × 0.000001

Area conversions:

• m²: Direct use
• cm²: m² = cm² × 0.0001
• mm²: m² = mm² × 0.000001

Velocity conversions for display:

• cm/s: m/s × 100
• mm/s: m/s × 1000

Display format:

• If a velocity value is less than 0.00001 (and greater than 0), it is displayed in scientific notation (e.g., \( 1.234567e-12 \)).
• Otherwise, it is displayed in decimal format with fixed decimal places (12 for m/s, 6 for cm/s and mm/s).

Explanation: The input current (\( I \)) is converted to amperes, the charge (\( Q \)) to coulombs, and the area (\( A \)) to square meters. The number of electrons per unit volume (\( n \)) is used directly in electrons/m³. The drift velocity is calculated in meters per second (m/s) using the precise value of the elementary charge (\( e = 1.60217662 \times 10^{-19} \, \text{C} \)) for accuracy, and then converted to centimeters per second (cm/s) and millimeters per second (mm/s) for display. Small values are shown in scientific notation for clarity.

3. Importance of Drift Velocity Calculation

Details: Drift velocity represents the average speed at which electrons move in a conductor due to an electric field. It’s a fundamental concept in understanding electrical conduction, helping engineers and physicists analyze current flow, conductor resistance, and material properties.

4. Using the Calculator

Tips: Enter the flow of current (\( I \)) in A or mA, the charge of an electron (\( Q \)) in C or µC (default is \( 1.6 \times 10^{-19} \, \text{C} \), the elementary charge \( e \)), the number of electrons per unit volume (\( n \)) in electrons/m³ (default is \( 8.5 \times 10^{28} \, \text{electrons/m}^3 \) for copper), and the cross-sectional area (\( A \)) in m², cm², or mm². The result will be the drift velocity in meters per second (m/s), centimeters per second (cm/s), and millimeters per second (mm/s). Values less than 0.00001 will be displayed in scientific notation.

Examples:

• \( I = 1 \, \text{A}, \, Q = 1.6 \times 10^{-19} \, \text{C}, \, n = 8.5 \times 10^{28} \, \text{electrons/m}^3, \, A = 1 \, \text{mm}^2 \):
  • \( A = 0.000001 \, \text{m}^2 \)
  • \( \mu = \frac{1}{8.5 \times 10^{28} \cdot 1.60217662 \times 10^{-19} \cdot 0.000001} \approx 7.346941 \times 10^{-5} \, \text{m/s} = 0.007347 \, \text{cm/s} = 0.073469 \, \text{mm/s} \)
• \( I = 10 \, \text{mA}, \, Q = 1.6 \times 10^{-19} \, \text{C}, \, n = 8.5 \times 10^{28} \, \text{electrons/m}^3, \, A = 0.5 \, \text{mm}^2 \):
  • \( I = 0.01 \, \text{A}, \, A = 0.0000005 \, \text{m}^2 \)
  • \( \mu = \frac{0.01}{8.5 \times 10^{28} \cdot 1.60217662 \times 10^{-19} \cdot 0.0000005} \approx 2.938776 \times 10^{-5} \, \text{m/s} = 0.002939 \, \text{cm/s} = 0.029388 \, \text{mm/s} \)
• \( I = 0.1 \, \text{A}, \, Q = 1.6 \times 10^{-19} \, \text{C}, \, n = 8.5 \times 10^{28} \, \text{electrons/m}^3, \, A = 1 \, \text{cm}^2 \):
  • \( A = 0.0001 \, \text{m}^2 \)
  • \( \mu = \frac{0.1}{8.5 \times 10^{28} \cdot 1.60217662 \times 10^{-19} \cdot 0.0001} \approx 7.346941 \times 10^{-6} \, \text{m/s} = 0.000735 \, \text{cm/s} = 0.007347 \, \text{mm/s} \)
• \( I = 0.001 \, \text{A}, \, Q = 1.6 \times 10^{-19} \, \text{C}, \, n = 8.5 \times 10^{28} \, \text{electrons/m}^3, \, A = 1 \, \text{m}^2 \):
  • \( \mu = \frac{0.001}{8.5 \times 10^{28} \cdot 1.60217662 \times 10^{-19} \cdot 1} \approx 7.346941 \times 10^{-11} \, \text{m/s} = 7.346941e-11 \, \text{m/s} = 7.346941e-09 \, \text{cm/s} = 7.346941e-08 \, \text{mm/s} \)

5. Frequently Asked Questions (FAQ)

Q: What is drift velocity?
A: Drift velocity (\( \mu \)) is the average velocity of electrons moving through a conductor due to an electric field. It’s typically very small (on the order of \( 10^{-5} \) to \( 10^{-3} \, \text{m/s} \)) because electrons move randomly but experience a net drift in the direction of the current.

Q: Why must charge, electron density, and area be greater than zero?
A: The formula involves dividing by \( n \), \( Q \), and \( A \). If any of these values are zero, the calculation would involve division by zero, which is undefined in mathematics.

Q: What are typical values for the charge of an electron and electron density?
A: The charge of an electron (\( Q \)) is approximately \( 1.6 \times 10^{-19} \, \text{C} \) (precisely \( 1.60217662 \times 10^{-19} \, \text{C} \)). The electron density (\( n \)) depends on the material; for copper, it’s approximately \( 8.5 \times 10^{28} \, \text{electrons/m}^3 \).

Q: Why are small velocity values displayed in scientific notation?
A: Velocities less than 0.00001 (e.g., \( 1 \times 10^{-5} \)) are displayed in scientific notation for clarity, as they are very small and would otherwise show as long strings of zeros in decimal format (e.g., 0.00000000007346941 m/s becomes \( 7.346941e-11 \, \text{m/s} \)).

Q: Why is the velocity displayed in multiple units (m/s, cm/s, mm/s)?
A: Drift velocities are often very small, so displaying the result in meters per second (m/s), centimeters per second (cm/s), and millimeters per second (mm/s) provides flexibility for different applications, making the values more readable depending on the scale.

Drift Velocity Calculator© - All Rights Reserved 2025