Ideal Transformer Calculator

Calculate:

Primary Voltage (V_p):

Secondary Voltage Unit (V_s):

Primary Turns (N_p):

Secondary Turns (N_s):

Secondary Current (I_s, ):

1. What is an Ideal Transformer Calculator?

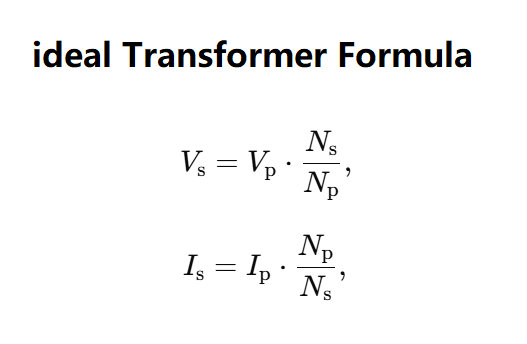
Definition: This calculator computes the secondary voltage (\( V_s \)) or secondary current (\( I_s \)) for an ideal transformer, which transfers electrical energy between two coils (primary and secondary) with no losses, using the relationships between voltages, currents, and the number of turns.

Purpose: It is used in electrical engineering to design transformers for applications such as power distribution, voltage regulation, and impedance matching.

2. How Does the Calculator Work?

The calculator uses the following equations for an ideal transformer:

\( V_s = V_p \cdot \frac{N_s}{N_p} \)
\( I_s = I_p \cdot \frac{N_p}{N_s} \)

Where:

\( V_s \) is the secondary voltage (V)
\( V_p \) is the primary voltage (V)
\( N_s \) is the number of turns in the secondary coil
\( N_p \) is the number of turns in the primary coil
\( I_s \) is the secondary current (A)
\( I_p \) is the primary current (A)

Steps:

Select the parameter to calculate (\( V_s \) or \( I_s \))
For \( V_s \), enter the primary voltage (\( V_p \)), primary turns (\( N_p \)), and secondary turns (\( N_s \))
For \( I_s \), enter the primary current (\( I_p \)), primary turns (\( N_p \)), and secondary turns (\( N_s \))
Convert inputs to base units (V for voltages, A for currents)
Calculate the selected parameter using the appropriate equation
Convert the result back to the user-specified unit

Display format:

If a value is > 10000 or < 0.0001 (and not zero), use scientific notation (e.g., \( 1.23456e-3 \))
Otherwise, display with 5 decimal places

3. Importance of Ideal Transformer Calculation

Details: Ideal transformer calculations are crucial for designing transformers in power systems, ensuring proper voltage and current transformation for efficient energy transfer and impedance matching.

4. Using the Calculator

Tips: Ensure all inputs are positive for the number of turns and non-negative for voltages and currents. The calculator assumes an ideal transformer with no losses, which is a simplification of real-world transformers.

Examples:

Calculate Secondary Voltage: \( V_p = 230 \, \text{V} \), \( N_p = 1000 \), \( N_s = 100 \):
- \( V_s = 230 \cdot \frac{100}{1000} = 23.00000 \, \text{V} \)
Calculate Secondary Current: \( I_p = 2 \, \text{A} \), \( N_p = 500 \), \( N_s = 100 \):
- \( I_s = 2 \cdot \frac{500}{100} = 10.00000 \, \text{A} \)

5. Frequently Asked Questions (FAQ)

Q: What is an ideal transformer?
A: An ideal transformer is a theoretical model that transfers electrical energy between two coils with no losses, following the voltage and current relationships based on the turns ratio.

Q: Why is the turns ratio important?
A: The turns ratio (\( N_s / N_p \)) determines the voltage and current transformation between the primary and secondary coils, allowing for step-up or step-down voltage conversion.

Q: How does an ideal transformer differ from a real transformer?
A: An ideal transformer assumes no losses (e.g., no resistance, leakage flux, or core losses), while real transformers have inefficiencies that affect performance.

Favorite