Power from Work and Duration Calculator

Work (W):

Duration (Δt):

Power (W): Power (N·m/s): Power (ft·lbf/s): Power (kW): Power (MW):

1. What is a Power from Work and Duration Calculator?

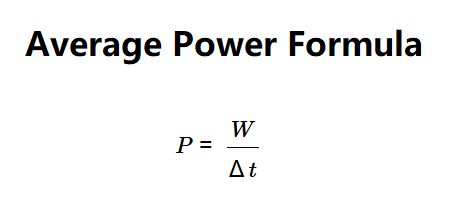
Definition: This calculator computes the power (\( P \)) based on the work done (\( W \)) and the duration (\( \Delta t \)) over which the work is performed.

Purpose: It is used in physics and engineering to determine the rate of energy transfer or work done, which is essential in applications like mechanical systems, electrical circuits, and energy analysis.

2. How Does the Calculator Work?

Power is calculated using:

\[ P = \frac{W}{\Delta t} \]

Work conversions:

N·m: Direct use
J: N·m (same as Joule)
ft·lbf: N·m = ft·lbf × 1.3558179483314
kJ: N·m = kJ × 1000
MJ: N·m = MJ × 1,000,000
kWh: N·m = kWh × 3,600,000
MWh: N·m = MWh × 3,600,000,000

Duration conversions:

s: Direct use
ms: s = ms × 0.001
µs: s = µs × 0.000001
ns: s = ns × 0.000000001
min: s = min × 60
h: s = h × 3600

Power conversions for display:

N·m/s: Same as W
ft·lbf/s: W ÷ 1.3558179483314
kW: W ÷ 1000
MW: W ÷ 1,000,000

Explanation: The input work is converted to newton-meters (N·m, equivalent to joules), and the duration is converted to seconds. Power is then calculated by dividing work by duration, resulting in watts (W). The result is also converted to N·m/s, ft·lbf/s, kilowatts (kW), and megawatts (MW) for display.

3. Importance of Power Calculation

Details: Power is a fundamental concept in physics, representing the rate at which work is done or energy is transferred. It’s crucial for designing efficient systems, such as engines, motors, and electrical devices, and for analyzing energy consumption.

4. Using the Calculator

Tips: Enter the work (\( W \)) in N·m, J, ft·lbf, kJ, MJ, kWh, or MWh, and the duration (\( \Delta t \)) in s, ms, µs, ns, min, or h (duration must be greater than 0). The result will be the power in watts (W), N·m/s, ft·lbf/s, kilowatts (kW), and megawatts (MW).

Examples:

\( W = 1000 \, \text{J}, \, \Delta t = 2 \, \text{s} \): \( P = \frac{1000}{2} = 500 \, \text{W} = 500 \, \text{N·m/s} = 368.781 \, \text{ft·lbf/s} = 0.5 \, \text{kW} = 0.0005 \, \text{MW} \)
\( W = 1 \, \text{kJ}, \, \Delta t = 1 \, \text{ms} \): \( P = \frac{1000}{0.001} = 1000000 \, \text{W} = 1000000 \, \text{N·m/s} = 737562.149 \, \text{ft·lbf/s} = 1000 \, \text{kW} = 1 \, \text{MW} \)
\( W = 1355.818 \, \text{ft·lbf}, \, \Delta t = 1 \, \text{s} \): \( P = \frac{1355.818 \times 1.3558179483314}{1} \approx 1839.905 \, \text{W} = 1839.905 \, \text{N·m/s} = 1355.818 \, \text{ft·lbf/s} = 1.840 \, \text{kW} = 0.001840 \, \text{MW} \)
\( W = 1 \, \text{kWh}, \, \Delta t = 1 \, \text{h} \): \( P = \frac{3600000}{3600} = 1000 \, \text{W} = 1000 \, \text{N·m/s} = 737.562 \, \text{ft·lbf/s} = 1 \, \text{kW} = 0.001 \, \text{MW} \)

5. Frequently Asked Questions (FAQ)

Q: What does power represent in this context?
A: Power (\( P \)) represents the rate at which work is done or energy is transferred, measured in watts (W). It’s calculated as work (\( W \)) divided by the time duration (\( \Delta t \)).

Q: Why is duration not allowed to be zero?
A: The formula involves dividing by duration (\( \Delta t \)). If duration is zero, the calculation would involve division by zero, which is undefined in mathematics.

Q: What are typical units for work and duration?
A: Work is typically measured in newton-meters (N·m) or joules (J), but units like ft·lbf, kJ, MJ, kWh, and MWh are also common. Duration is often in seconds (s), but smaller units like µs and ns, or larger units like minutes and hours, are used depending on the application.

Q: Why is the result displayed in multiple units (W, N·m/s, ft·lbf/s, kW, MW)?
A: Displaying power in multiple units provides flexibility for different applications. Watts (W) and N·m/s are standard SI units, ft·lbf/s is common in imperial systems, and kW and MW are used for larger scales like electrical systems or power plants.

Q: How does duration affect the power value?
A: Power is inversely proportional to duration. For a fixed amount of work, a shorter duration (e.g., in µs or ns) results in higher power, while a longer duration (e.g., in hours) results in lower power. For example, 1000 J in 1 s gives 1000 W, but in 1 ms, it gives 1,000,000 W.

Favorite