1. What is an RC Time Constant Calculator?

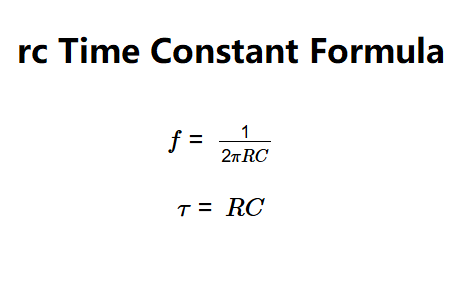
Definition: This calculator computes the characteristic frequency (\( f \)), resistance (\( R \)), capacitance (\( C \)), or time constant (\( \tau \)) for an RC circuit, which consists of a resistor and capacitor in series.

Purpose: It is used in electronics to analyze RC circuits, determine the frequency response, and calculate the time constant for applications such as filters, timers, and signal processing.

2. How Does the Calculator Work?

The calculator uses the following equations for an RC circuit:

Where:

• \( f \) is the characteristic frequency (Hz)
• \( R \) is the resistance (Ω)
• \( C \) is the capacitance (F)
• \( \tau \) is the time constant (s)

Steps:

• Select the parameter to calculate (\( f \), \( R \), \( C \), or \( \tau \))
• Enter the known values (e.g., resistance and capacitance for frequency)
• Convert inputs to base units (Ω for resistance, F for capacitance, Hz for frequency, s for time)
• Calculate the selected parameter using the appropriate equation
• Convert the result back to the user-specified unit

Display format:

• If a value is > 10000 or < 0.0001 (and not zero), use scientific notation (e.g., \( 1.23456e-3 \))
• Otherwise, display with 5 decimal places

3. Importance of RC Time Constant Calculation

Details: The RC time constant and characteristic frequency are critical in designing RC circuits for applications like filters, timers (e.g., 555 timer circuits), and signal processing, determining how quickly a capacitor charges or discharges.

4. Using the Calculator

Tips: Ensure all inputs are positive for resistance, capacitance, and frequency. The calculator assumes a simple RC circuit with no additional components affecting the time constant.

Examples:

• Calculate Characteristic Frequency: \( R = 1 \, \text{kΩ} \), \( C = 1 \, \text{µF} \):
  • \( f = \frac{1}{2\pi \times 1000 \times 1 \times 10^{-6}} = 159.15494 \, \text{Hz} \)
• Calculate Resistance: \( f = 1 \, \text{kHz} \), \( C = 0.1 \, \text{µF} \):
  • \( R = \frac{1}{2\pi \times 1000 \times 0.1 \times 10^{-6}} = 1591.54943 \, \text{Ω} \)
• Calculate Capacitance: \( f = 500 \, \text{Hz} \), \( R = 2 \, \text{kΩ} \):
  • \( C = \frac{1}{2\pi \times 500 \times 2000} = 0.00016 \, \text{F} = 159.15494 \, \text{µF} \)
• Calculate Time Constant: \( R = 1 \, \text{kΩ} \), \( C = 1 \, \text{µF} \):
  • \( \tau = 1000 \times 1 \times 10^{-6} = 0.00100 \, \text{s} = 1.00000 \, \text{ms} \)

5. Frequently Asked Questions (FAQ)

Q: What is the RC time constant?
A: The RC time constant (\( \tau \)) is the time it takes for the voltage across a capacitor in an RC circuit to charge to approximately 63.2% of its final value, given by \( \tau = RC \).

Q: What is the characteristic frequency of an RC circuit?
A: The characteristic frequency (\( f \)) is the frequency at which the impedance of the RC circuit changes significantly, given by \( f = \frac{1}{2\pi RC} \).

Q: How is the RC time constant used in 555 timer circuits?
A: In 555 timer circuits, the RC time constant determines the timing intervals for oscillations or delays, controlling the frequency and duty cycle of the output signal.

RC Time Constant Calculator© - All Rights Reserved 2025