1. What is an RF Power to Voltage Calculator?

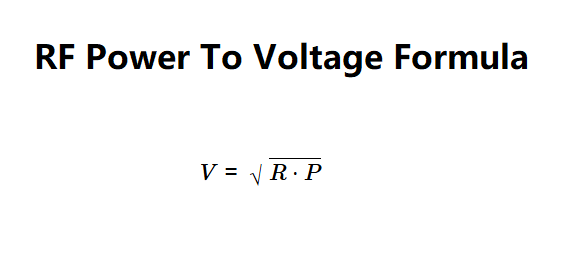
Definition: This calculator converts RF power (P) and impedance (R) into voltage in volts, millivolts, and microvolts.

Purpose: It is used in RF engineering, telecommunications, and electronics to determine the voltage across a load given the power and impedance of the system.

2. How Does the Calculator Work?

Voltage is calculated using:

Power conversions:

• W: Direct use
• mW: W = mW × 0.001
• µW: W = µW × 0.000001

Impedance conversions:

• Ω: Direct use
• kΩ: Ω = kΩ × 1000
• MΩ: Ω = MΩ × 1,000,000

Voltage conversions for display:

• mV: V × 1000
• µV: V × 1,000,000

Explanation: The input power is converted to watts, and the impedance is converted to ohms. The voltage is then calculated using the relationship \( V = \sqrt{R \cdot P} \). The result is converted to millivolts and microvolts for additional display.

3. Importance of Voltage Calculation

Details: Converting RF power to voltage is essential in RF systems for determining the actual voltage across a load, which is necessary for designing and analyzing circuits, amplifiers, and communication systems.

4. Using the Calculator

Tips: Enter the RF power (P) in W, mW, or µW (power must be non-negative) and the impedance in Ω, kΩ, or MΩ (impedance must be greater than 0). The result will be the voltage in volts (V), millivolts (mV), and microvolts (µV).

Examples (assuming R = 50 Ω):

• 1 W: \( V = \sqrt{50 \cdot 1} = \sqrt{50} \approx 7.071 \, \text{V} = 7071 \, \text{mV} = 7,071,068 \, \text{µV} \)
• 1 mW: \( V = \sqrt{50 \cdot 0.001} = \sqrt{0.05} \approx 0.224 \, \text{V} = 224 \, \text{mV} = 223,607 \, \text{µV} \)
• 2 mW: \( V = \sqrt{50 \cdot 0.002} = \sqrt{0.1} \approx 0.316 \, \text{V} = 316 \, \text{mV} = 316,228 \, \text{µV} \)
• 1 µW: \( V = \sqrt{50 \cdot 0.000001} = \sqrt{0.00005} \approx 0.007 \, \text{V} = 7.071 \, \text{mV} = 7,071 \, \text{µV} \)

5. Frequently Asked Questions (FAQ)

Q: Why is impedance required for this calculation?
A: Impedance is needed because voltage depends on both power and resistance via the relationship \( V = \sqrt{R \cdot P} \). Without knowing the impedance, the voltage cannot be determined from power alone.

Q: Why is the impedance not allowed to be zero?
A: If impedance is zero, the voltage would be zero (since \( V = \sqrt{0 \cdot P} = 0 \)), which is not practical for most RF applications. Additionally, zero impedance can imply a short circuit, which is typically invalid in this context.

Q: Why is the power not allowed to be negative?
A: Power cannot be negative in this context, as it represents a physical quantity (energy per unit time). A negative power would result in an imaginary voltage (since the square root of a negative number is not real), which is not meaningful here.

Q: Why does the calculator default to 50 Ω for impedance?
A: 50 Ω is a standard impedance in RF systems, commonly used in antennas, transmission lines, and test equipment. It’s a typical value for many applications, but you can adjust it as needed.

Q: How does impedance affect the voltage?
A: Voltage is proportional to the square root of impedance. For example, doubling the impedance (e.g., from 50 Ω to 100 Ω) increases the voltage by a factor of \( \sqrt{2} \approx 1.414 \), assuming the power remains constant.

RF Power to Voltage Calculator© - All Rights Reserved 2025