1. What is a Sallen-Key Filter Calculator?

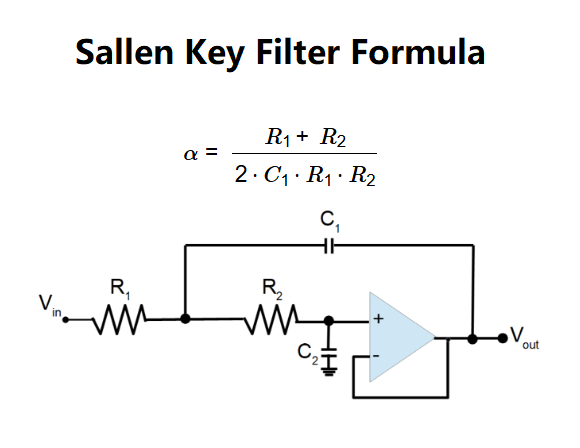
Definition: This calculator computes the damping factor (\( \alpha \)) for a Sallen-Key filter, a type of active filter used in electronics.

Purpose: It is used in circuit design to determine the damping factor, which influences the filter's frequency response and stability, such as in low-pass or high-pass filter configurations.

2. How Does the Calculator Work?

The damping factor is calculated using:

Resistance conversions:

• Ω: Direct use
• kΩ: Ω = kΩ × 1000
• MΩ: Ω = MΩ × 1,000,000

Capacitance conversions:

• F: Direct use
• µF: F = µF × 0.000001
• nF: F = nF × 0.000000001
• pF: F = pF × 0.000000000001

Explanation: The input resistances are converted to ohms, and the capacitance is converted to farads. The damping factor \( \alpha \) is then computed using the given formula, which determines the filter's behavior (e.g., Butterworth, Chebyshev, or Bessel response).

3. Importance of Damping Factor Calculation

Details: The damping factor \( \alpha \) is critical in Sallen-Key filter design as it affects the filter's Q-factor, bandwidth, and transient response. It helps engineers tune the filter for specific applications, such as audio processing or signal conditioning.

4. Using the Calculator

Tips: Enter Resistance 1 (\( R_1 \)) and Resistance 2 (\( R_2 \)) in Ω, kΩ, or MΩ, and Capacitance 1 (\( C_1 \)) in F, µF, nF, or pF (all values must be greater than 0). The result will be the damping factor \( \alpha \).

Examples:

• \( R_1 = 10 \, \text{kΩ}, \, R_2 = 10 \, \text{kΩ}, \, C_1 = 1 \, \text{nF} \): \( \alpha = \frac{10000 + 10000}{2 \cdot 1 \times 10^{-9} \cdot 10000 \cdot 10000} = \frac{20000}{2 \times 10^{-9} \cdot 10^8} = \frac{20000}{0.2} = 100000 \)
• \( R_1 = 5 \, \text{kΩ}, \, R_2 = 5 \, \text{kΩ}, \, C_1 = 100 \, \text{nF} \): \( \alpha = \frac{5000 + 5000}{2 \cdot 100 \times 10^{-9} \cdot 5000 \cdot 5000} = \frac{10000}{2 \times 10^{-7} \cdot 25 \times 10^6} = \frac{10000}{5 \times 10^{-1}} = 20000 \)
• \( R_1 = 1 \, \text{kΩ}, \, R_2 = 2 \, \text{kΩ}, \, C_1 = 47 \, \text{nF} \): \( \alpha = \frac{1000 + 2000}{2 \cdot 47 \times 10^{-9} \cdot 1000 \cdot 2000} = \frac{3000}{2 \times 47 \times 10^{-9} \cdot 2 \times 10^6} = \frac{3000}{188 \times 10^{-3}} \approx 15957.447 \)

5. Frequently Asked Questions (FAQ)

Q: What is the damping factor in a Sallen-Key filter?
A: The damping factor \( \alpha \) determines the shape of the filter's frequency response. It affects the Q-factor and the filter's behavior, such as whether it exhibits a Butterworth (\( \alpha = \sqrt{2} \)), Chebyshev, or Bessel response.

Q: Why are resistances and capacitance not allowed to be zero?
A: The formula involves dividing by \( R_1 \), \( R_2 \), and \( C_1 \). If any of these values are zero, the calculation would involve division by zero, which is undefined in mathematics.

Q: What are typical values for \( R_1 \), \( R_2 \), and \( C_1 \)?
A: In practical Sallen-Key filters, resistances are often in the range of 1 kΩ to 100 kΩ, and capacitances are typically in the range of 1 nF to 100 nF, depending on the desired cutoff frequency and filter type.

Q: How does the damping factor affect the filter's performance?
A: A higher \( \alpha \) results in a lower Q-factor, leading to a more damped response (less peaking near the cutoff frequency). A lower \( \alpha \) increases the Q-factor, which can cause peaking or even oscillation if too low.

Q: Can this calculator be used for high-pass Sallen-Key filters?
A: Yes, the damping factor \( \alpha \) applies to both low-pass and high-pass Sallen-Key filters, as it is a fundamental parameter of the filter's topology. However, the interpretation of \( \alpha \) in terms of frequency response may differ depending on the filter type.

Sallen-Key Filter Calculator© - All Rights Reserved 2025