1. What is a dBm to Voltage Calculator?

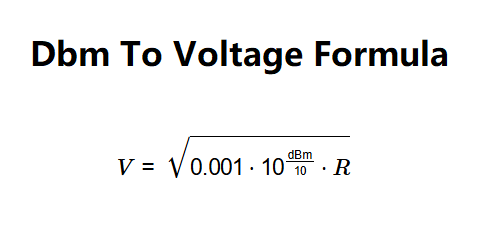
Definition: This calculator converts a power level in dBm (decibels relative to 1 milliwatt) and an impedance value into voltage in volts, millivolts, and microvolts.

Purpose: It is used in RF engineering, telecommunications, and electronics to determine the voltage across a load given a power level in dBm and the impedance of the system.

2. How Does the Calculator Work?

Voltage is calculated using:

Impedance conversions:

• Ω: Direct use
• kΩ: Ω = kΩ × 1000
• MΩ: Ω = MΩ × 1,000,000

Voltage conversions for display:

• mV: V × 1000
• µV: V × 1,000,000

Explanation: The dBm value is first converted to power in watts using \( P = 0.001 \cdot 10^{\frac{\text{dBm}}{10}} \). Then, the voltage is calculated using the relationship \( V = \sqrt{P \cdot R} \), where \( R \) is the impedance in ohms. The result is then converted to millivolts and microvolts for additional display.

3. Importance of Voltage Calculation

Details: Converting dBm to voltage is essential in RF systems for determining the actual voltage across a load, which is necessary for designing and analyzing circuits, amplifiers, and communication systems.

4. Using the Calculator

Tips: Enter the power level in dBm and the impedance in Ω, kΩ, or MΩ (impedance must be greater than 0). The result will be the voltage in volts (V), millivolts (mV), and microvolts (µV).

Examples (assuming R = 50 Ω):

• 30 dBm: \( P = 0.001 \cdot 10^{\frac{30}{10}} = 1 \, \text{W}, \, V = \sqrt{1 \cdot 50} = \sqrt{50} \approx 7.071 \, \text{V} = 7071 \, \text{mV} = 7,071,068 \, \text{µV} \)
• 0 dBm: \( P = 0.001 \cdot 10^{\frac{0}{10}} = 0.001 \, \text{W}, \, V = \sqrt{0.001 \cdot 50} = \sqrt{0.05} \approx 0.224 \, \text{V} = 224 \, \text{mV} = 223,607 \, \text{µV} \)
• 3.01 dBm: \( P = 0.001 \cdot 10^{\frac{3.01}{10}} \approx 0.002 \, \text{W}, \, V = \sqrt{0.002 \cdot 50} = \sqrt{0.1} \approx 0.316 \, \text{V} = 316 \, \text{mV} = 316,228 \, \text{µV} \)
• -30 dBm: \( P = 0.001 \cdot 10^{\frac{-30}{10}} = 0.000001 \, \text{W}, \, V = \sqrt{0.000001 \cdot 50} = \sqrt{0.00005} \approx 0.007 \, \text{V} = 7.071 \, \text{mV} = 7,071 \, \text{µV} \)

5. Frequently Asked Questions (FAQ)

Q: Why is impedance required for this calculation?
A: Impedance is needed because voltage depends on both power and resistance via the relationship \( V = \sqrt{P \cdot R} \). Without knowing the impedance, the voltage cannot be determined from power alone.

Q: Why is the impedance not allowed to be zero?
A: If impedance is zero, the voltage would be zero (since \( V = \sqrt{P \cdot 0} = 0 \)), which is not practical for most RF applications. Additionally, zero impedance can imply a short circuit, which is typically invalid in this context.

Q: Can I use this calculator for dBW instead of dBm?
A: No, this calculator is designed for dBm (reference 1 mW). For dBW, the reference power is 1 W, so the formula would be \( V = \sqrt{1 \cdot 10^{\frac{\text{dBW}}{10}} \cdot R} \), which requires a different calculator.

Q: What does a negative dBm value mean in terms of voltage?
A: A negative dBm value indicates a power less than 1 mW, which results in a lower voltage. For example, -30 dBm with 50 Ω impedance gives a voltage of approximately 7.071 mV, compared to 0 dBm, which gives 224 mV.

Q: How do I interpret a dBm value of 0 dBm in terms of voltage?
A: A dBm value of 0 dBm means the power is 1 mW. With an impedance of 50 Ω, this results in a voltage of approximately 0.224 V (224 mV). The voltage scales with the square root of power and impedance.

dBm to Voltage Calculator© - All Rights Reserved 2025